How to Calculate Poker Combinations and Probability?

In mathematics, combinatorics, also called combinatorial analysis, studies configurations of finite collections of objects or combinations of finite sets, and their counting.

While this might sound complex at first glance, it's much simpler than it appears and is especially useful in poker hand analysis. To explain the basics of combinatorics, we'll use a very simple situation that you might encounter in live Texas Hold'em poker tournaments.

We're participating in a 6-max tournament in a perfect setting:

• swimming pool
• music
• cards...

Everything is perfect, including the presence of none other than Davidi Kitai. A talented player capable of anything, especially winning our chips with disconcerting ease if he happens to be seated next to us.

After more than 3 hours of play, we're on the right track with a stack exceeding 35,000 chips while the average stack is 21,000 chips. Our table breaks after a difficult final hand that damaged both our stack and our confidence.

We have 18,325 chips remaining and we're heading to our new table. We discover a table with only 3 players and therefore 3 empty seats. Two other players arrive to fill this 6-max table, and among them is Davidi!

All we can do now is hope not to be seated next to Davidi, which would be a real bad beat...

The Initial Situation

Here's everything we know:

• A 6-max table with 3 players already seated
• Players are seated randomly
• Davidi and ourselves must take our seats at the table

In the rest of the article, we'll study the seating arrangement of the players completing the table.

In probability theory, this is called a random experiment.
A random experiment is an observable experiment where the outcome cannot be predicted in advance, even if the experiment is repeated under identical conditions.

What's the Probability of Not Being Seated Next to Davidi?

If you're ready, our goal is to determine the probability of not being seated next to the ruthless Davidi.

Listing All Possible Combinations

To begin, we'll determine all existing combinations. With 3 people to place in 3 seats, nothing could be simpler! We just need to list them all.

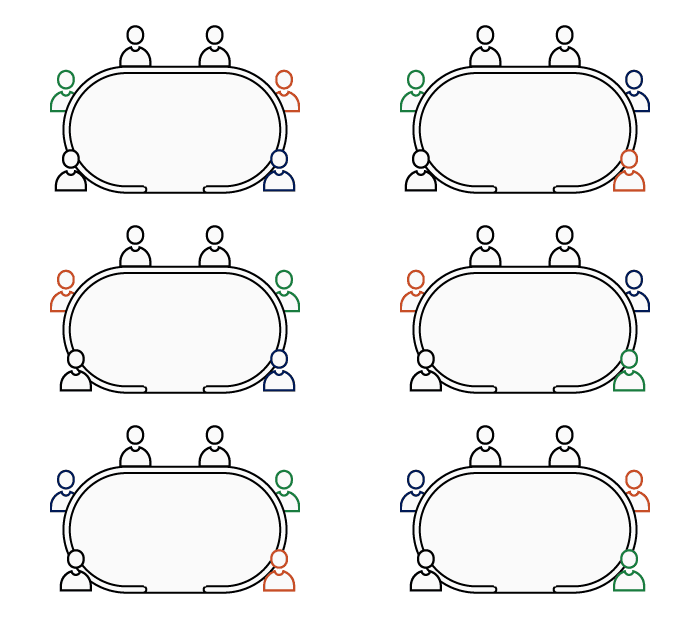
We get 6 possible combinations for placing 3 people in 3 seats. By listing them, we have just enumerated all possible combinations.

More specific combinations can be counted:

• combinations where we are seated next to Davidi
• combinations where we are not seated next to Davidi

Out of the 6 combinations:

• 2 times, we are seated next to Davidi
• 4 times, we are not seated next to Davidi

Therefore, we end up next to Davidi 2 times out of 6, and 4 times out of 6 we won't be.

In probability theory, we talk about events.
An event is a set of possible outcomes from a random experiment.
In our case, "sitting next to Davidi" is an event and "not sitting next to Davidi" is its complementary event.

The set of all possible outcomes of a random experiment is called the Universe and is often denoted

(read as Omega).

The probability of the event "sitting next to Davidi" is

The probability of the complementary event "not sitting next to Davidi" is

We notice that the probability of "sitting next to Davidi" (

Some Mathematical Notations to Simplify the Work

To facilitate further analysis, I'll introduce new mathematical concepts: the notation of probability, union, and intersection.

In the rest of the article, we'll name the events:

• : "sitting next to Davidi"
• : "Not sitting next to Davidi"
• : "being Seated at the table"

The probability of an event is denoted

The union of two events is denoted:

• "sitting next to Davidi" OR "not sitting next to Davidi"

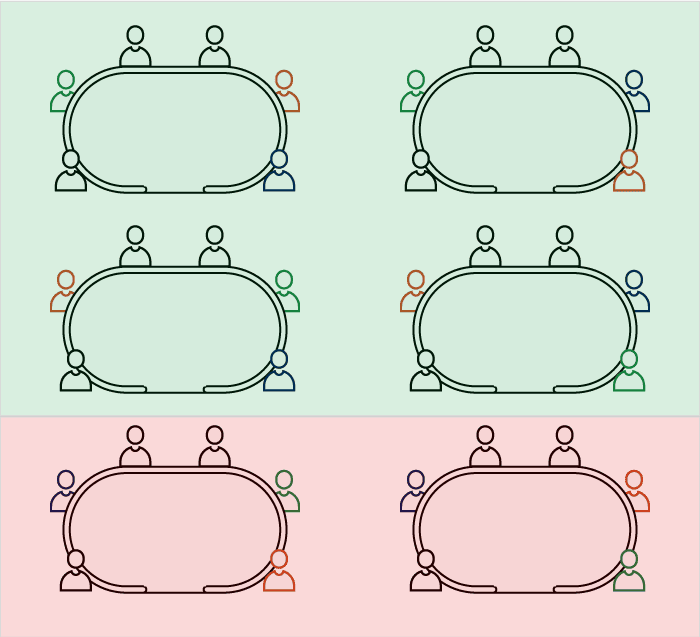
Here, we can see that the union of these two events corresponds to the set of all possible outcomes of this experiment.

The two events have no elements in common and all possible outcomes are covered, this is called a partition.

Here are 2 new events:

• : "Davidi sits in one of the two Right seats at the table"
• : "Hero sits in one of the two Right seats at the table"

The intersection of two events is denoted:

• "Davidi sits in one of the two right seats at the table" AND (simultaneously) "Hero sits in one of the two right seats at the table"

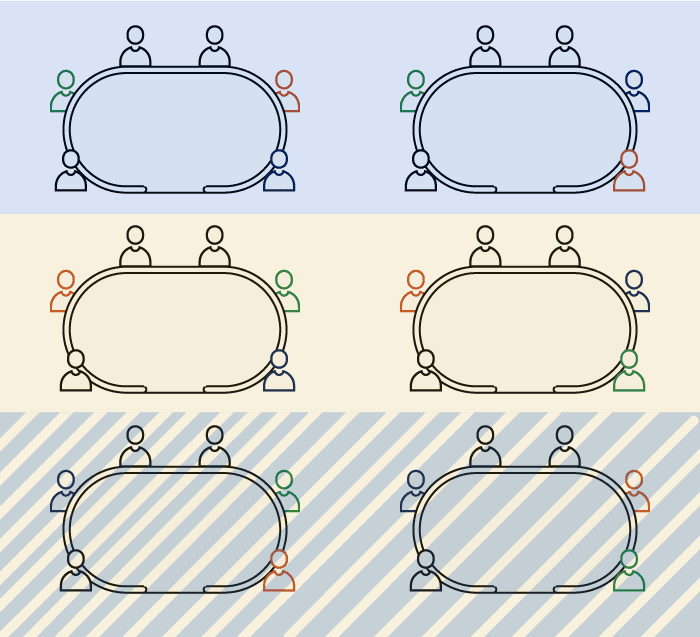
Here again, we can see that the union of these two events corresponds to the set of all possible outcomes of this experiment.
However, the two events have elements in common, which we call the intersection of these two events.
There are two combinations where Hero and Davidi are both located on the right side of the table.

The probability of

By definition, the elements present in the intersection (

We can also notice that the union of the two events

An event with a probability of 1 is called a certain event.
The union of an event and its complementary event gives a certain event.
An event and its complementary event have no elements in common and therefore an empty intersection; they are said to be disjoint.

In general, for 3 events A, B, and C, if:

Then:

Let's return to our basic question: What is the probability of not sitting next to Davidi?

• where D: "sitting next to Davidi"
• where ND: "Not sitting next to Davidi"
• where A: "being Seated at the table"

Finding the Same Results Mathematically

Our three events are linked together. We have:

We will definitely be seated at the table at the end of the random experiment.

Determining the Cardinality of Our Random Experiment's Universe

The cardinality of a set is the number of elements contained in that set.
If

, then

is composed of elements

, for a total of 5 elements.

In our example, the elements of our Universe are triplets of the form (Player in seat 1, in seat 2, in seat 3).
For example: (Hero, Villain, Davidi) means:

• Hero in seat 1
• Villain in seat 2
• Davidi in seat 3

We need to determine the total number of possible combinations when placing 3 people in 3 seats.

The first step is to place one of the three players in a first seat.
Each player corresponds to one possibility, which gives us 3 different placements.

The second step is to place one of the two remaining players in the second seat.
For each of the 3 possibilities, there are two new possibilities.
This gives us a total of 3 x 2 different placements at this stage.

The final step is to place the remaining player in the last seat.
There is only one possibility left.
This makes a total of 3 x 2 x 1 = 6 different placements.

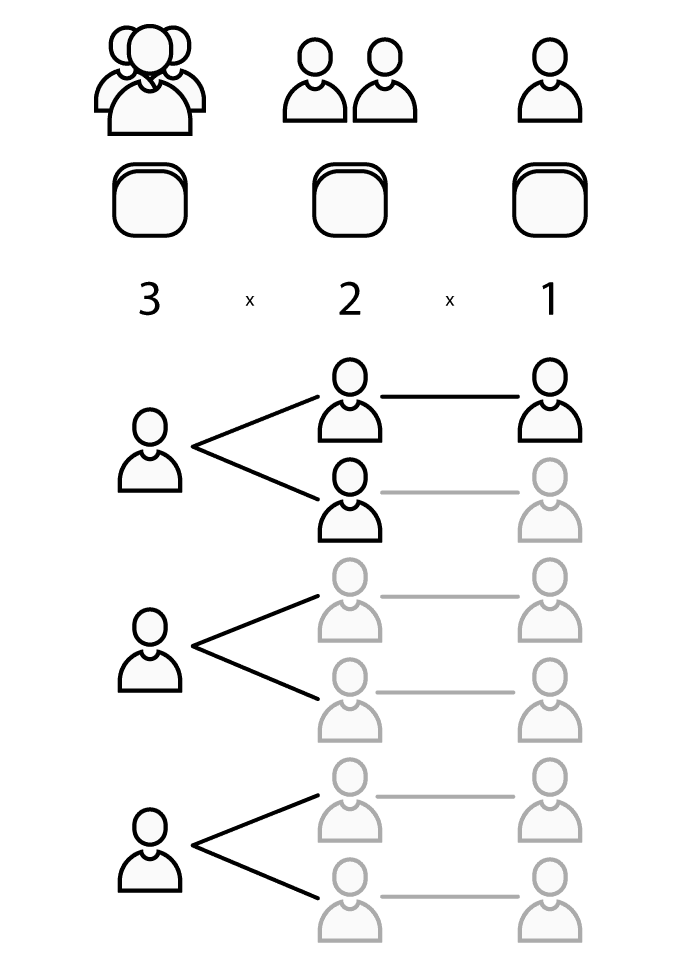
We therefore have 6 different placements where 3 players are placed in 3 seats, which is equivalent to saying: the cardinality of our random experiment's Universe is 6.

Determining the Cardinality of D

We can easily determine the combinations where we're seated next to Davidi without enumerating all possible cases.
Conversely, it's complicated to calculate the number of combinations where we're not next to Davidi.

For this reason, we aim to calculate the probability of being next to Davidi, and we'll simply subtract this probability from 1 to obtain the probability of not being next to Davidi.

The Starting Table

We begin by separating the 3 people to be placed into two groups:

• Us and Davidi
• The other Villain

Placing Villain

We can place Villain in the left seat. The person in this seat will inevitably be isolated from the other two players to be placed. Therefore, we cannot place either Davidi or ourselves there.

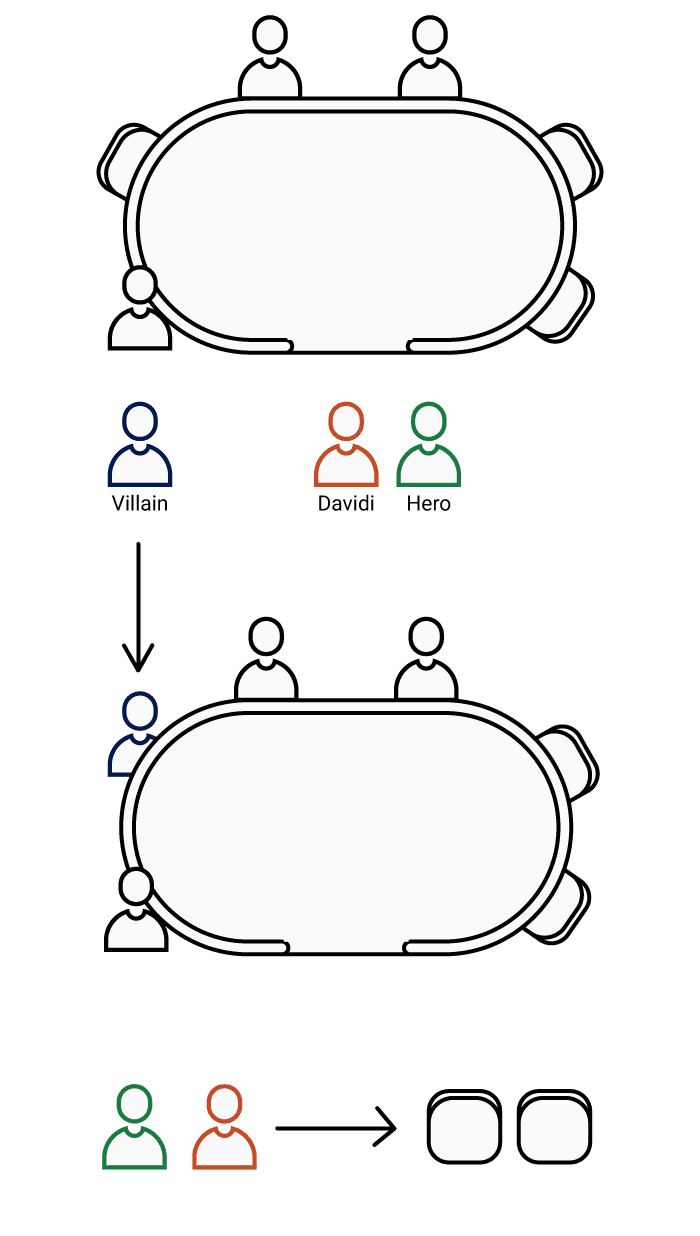
Calculating the Remaining Placements

Once Villain is placed, there are only two adjacent seats left and Davidi and ourselves to place. Since the order of placement matters, we're in the same case as before and find: 2 x 1 = 2 possible placements
Event D corresponds to two combinations, in other words

Determining the Probability of D

Event D corresponds to 2 combinations out of the 6 combinations that make up the Universe.
Event D will occur 2 times out of 6, which corresponds to a probability of

where

and

Determining the Probability of ND

Now that we know the probability of

Conclusion

The probability of event

Summary

• The concept of probability appears during a random experiment.
• An event is a set of possible outcomes.
• The cardinality of an event is the number of outcomes that compose it.
  Noted as:
• The probability of an event is the frequency at which the event will occur.
  Noted as:
• An event is certain when we are sure it will occur, meaning it has a probability of 1 (or 100%).
• The set of all possible outcomes of a random experiment is called the Universe.
• The union of an event and its complement (
  ) is equivalent to the Universe.

I'd Like a Pair of 10s or Better...

We'll try to determine the probability of being dealt a pair of 10s or better in an online poker hand, which is a good starting hand and could potentially lead to a set on the flop as a combination.

Here's all the information we have:

• a deck consists of 52 cards
• we receive 2 cards from the deck
• the cards are dealt randomly

Some formalism:

• event TT: being dealt a pair of 10s
• event TT+: being dealt a pair of 10s or better (i.e.: pair of 10s, Jacks, Queens, Kings, or Aces)

First Step: Drawing Two Cards from the 52-Card Deck

To begin, we need to calculate the number of combinations corresponding to drawing 2 cards from the 52 cards in the deck.
To draw two cards, we must first draw one card and then a second.
This might seem obvious, but I prefer to specify it anyway.

Drawing One Card from a 52-Card Deck

One possible draw would be pulling the Ace of hearts, another draw would be pulling the 2 of hearts... and so on for all 52 cards in the deck.
We can clearly see that one card corresponds to one possible draw. When drawing just one card from 52 cards, the number of possible draws is 52.

Drawing One Card from a 51-Card Deck

When we draw the first card, we don't put it back in the deck.
When drawing the second card, there are only 51 cards left in the deck. So we have 51 possible draws.

Drawing Two Cards from a 52-Card Deck

We have 52 draws corresponding to drawing a first card, then for each of these draws, we have 51 other possible draws.
This means there are 52 times 51 possible draws of two cards in a 52-card deck. That's

Arrangements and Combinations

During our different steps, a notion of order is present.
Drawing an Ace of hearts then a King of hearts is different from drawing a King of hearts then an Ace of hearts, yet it's the same hand.

The Concept of Arrangements

When choosing k elements from n and the notion of order is important, we get a k-tuple (an ordered list of k elements). This k-tuple is a k-arrangement.
We write

(read as "A" "n" "k"): the number of k-arrangements from n.

With our Ace of hearts and King of hearts, we have 2 arrangements for the same hand.

The Concept of Combination

When choosing k elements from n and the notion of order doesn't matter, we get a set of k elements. This set of k elements is a k-combination.
Written as

(read as "C" "n" "k") or

(read as "k" from "n"): the number of k-combinations from n.

A hand like Ace of hearts and King of hearts is a 2-combination.

Second Step: Combinations of Two Cards from 52

The Case of No Limit Hold'em

We have

We have 2652 2-arrangements of 2 cards from 52 cards.

One 2-combination (the hand Ace of hearts and King of hearts) corresponds to two 2-arrangements (Ace of hearts / King of hearts and King of hearts / Ace of hearts).
To get the number of 2-combinations, we need to divide the number of 2-arrangements by 2.

The Case of Pot Limit Omaha

In PLO, we don't receive 2 but 4 cards from 52 cards!
The goal is to determine the number of different hand combinations in PLO.

This amounts to asking: when 4 cards are drawn from a 52-card poker deck, how many combinations exist?

First step: Find the number of arrangements

Second step: Handle the notion of order

Third step: Find the number of combinations

A Bit of Mathematics

The Concept of Factorial

In mathematics, the factorial of a natural number k is the product of all positive integers less than or equal to k. (wikipedia.org)
It is written as:

(read as "k factorial")

Note:

Let's try to write our arrangements using factorials:

Let's try to write our combinations using factorials:

Thanks to these formulas, if we want to find the number of possible hand combinations in NLHE, we just need to calculate

Third Step: Being Dealt a Pair of 10s

We want to know the probability of being dealt a pair of 10s.
We're looking for

We have

To obtain

Fourth Step: Being Dealt a Pair of 10s or Better

Being dealt a pair of 10s or better means hitting one of these five pairs:

• TT
• JJ
• QQ
• KK
• AA

We saw that a pair of 10s corresponds to 6 hands because there are 4 ten cards in the deck. Since all pairs are composed the same way (2 cards from 4), each pair corresponds to 6 hands.
In our case, we have:

30 combos doesn't mean much to me...
No problem, let's convert it to a percentage!

And there you have it, in just a few steps, we've answered the original question!

Summary

• When we want to draw k elements from n elements with order in the draw, we get a k-arrangement which is an ordered list of k elements from n.
• We write
  , the number of k-arrangements of k elements from n.
• When we want to draw k elements from n elements without order in the draw, we get a k-combination which is an unordered list of k elements from n.
• We write
  , the number of k-combinations of k elements from n.