Comment calculer les combinaisons et la probabilité au poker ?
En mathématiques, la combinatoire, appelée aussi analyse combinatoire, étudie les configurations de collections finies d'objets ou les combinaisons d'ensembles finis, et les dénombrements.
C'est un peu barbare à la première lecture mais c'est beaucoup plus simple qu'il n'y parait et c'est surtout très utile dans l'analyse d'une main de Poker. Pour expliquer les bases de la combinatoire, on va se baser sur une situation très simple que vous pouvez rencontrer au Poker texas holdem lors de tournois live.

Nous sommes en train de participer à un tournois 6-max dans un cadre parfait :
- piscine
- musique
- cartes...
Tout est au rendez vous, même un certain Davidi Kitai. Un joueur de talent capable de tout et surtout de gagner nos jetons avec une facilité déconcertante s'il se trouve à côté de nous.
Après plus de 3 heures de jeu, nous sommes dans la bonne voie avec un stack qui dépasse les 35 000 jetons alors que le tapis moyen est de 21 000 jetons. Notre table casse après une dernière main difficile qui a mis à mal notre stack et notre confiance.
Il nous reste 18 325 jetons et nous nous dirigeons vers notre nouvelle table. Nous découvrons une table avec seulement 3 joueurs et donc 3 places libres. Deux autres joueurs se présentent pour remplir cette table de 6-max et parmi eux, il y a Davidi !
Il ne nous reste plus qu'à espérer ne pas être à côté de Davidi ce qui serait un véritable bad beat…
La situation de départ
Voici tout ce que nous savons :
- Une table de 6-max avec 3 joueurs déjà installés
- Les joueurs sont placés aléatoirement
- Davidi et nous-même devons nous installer à la table

Dans la suite de l'article, nous allons étudier le placement des joueurs comblant la table.
En probabilités, on parle d'expérience aléatoire.
Une expérience aléatoire est une expérience observable dont le résultat ne peut pas être prévu à l'avance même si l'expérience est répétée dans des conditions identiques.
Quelle est la probabilité de ne pas s'asseoir à côté de Davidi ?
Si tu l'acceptes, l'objectif est de déterminer la probabilité de ne pas nous asseoir à côté de l'impitoyable Davidi.
Énumérer les différentes combinaisons possibles
Pour commencer, nous déterminons toutes les combinaisons existantes. Avec 3 personnes à placer sur 3 sièges, rien de plus simple ! Il suffit de toutes les énumérer.
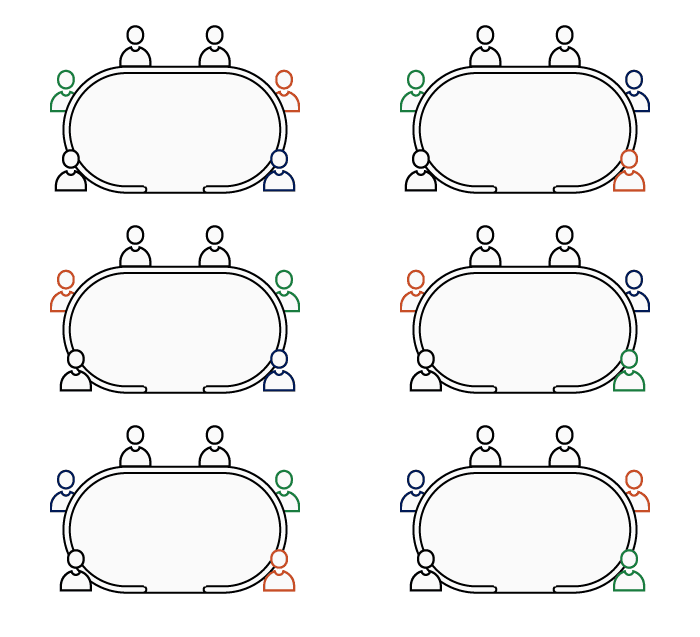
Nous obtenons 6 combinaisons possibles pour placer 3 personnes sur 3 sièges. En les énumérant, nous venons de dénombrer toutes les combinaisons possibles.
Des combinaisons plus précises peuvent être dénombrées :
- les combinaisons où nous sommes assis à côté de Davidi
- les combinaisons où nous ne sommes pas assis à côté de Davidi
Sur les 6 combinaisons :
- 2 fois, nous sommes assis à côté de Davidi
- 4 fois, nous ne sommes pas assis à côté de Davidi
Nous nous retrouvons donc 2 fois sur 6 à côté de Davidi et 4 fois sur 6 nous ne le serons pas.
En probabilités, on parle d'événements.
Un événement est un ensemble de résultats possibles d'une expérience aléatoire.
Dans notre cas, "s'asseoir à côté de Davidi" est un événement et "ne pas s'asseoir à côté de Davidi" est son événement contraire.
L'ensemble de tous les résultats possibles d'une expérience aléatoire s'appelle l'Univers et est souvent noté (qui se lit Oméga)..
La probabilité de l'événement "s'asseoir à côté de Davidi" est de
que l'on peut simplifier par . du temps, nous seront assis à côté de Davidi.La probabilité de l'événement contraire "ne pas s'asseoir à côté de Davidi" est de
soit . du temps, nous ne seront pas assis à côté de Davidi.On remarque que la probabilité de "s'asseoir à côté de Davidi" (
) ou de "ne pas s'asseoir à côté de Davidi" () est de . du temps, nous seront assis à la table (à côté de Davidi ou pas).Quelques notations mathématiques pour faciliter le travail
Pour faciliter la suite de la réflexion, je vais introduire de nouvelles notions mathématiques : la notation de la probabilité, l'union et l'intersection.
Dans la suite de l'article, nous nommerons les événements :
- : "s'asseoir à côté de Davidi"
- : "Ne pas s'asseoir à côté de Davidi"
- :"être Assis à la table"
La probabilité d'un événement est noté
.L'union de deux événements est noté :
- "s'asseoir à côté de Davidi" OU "ne pas s'asseoir à côté de Davidi"
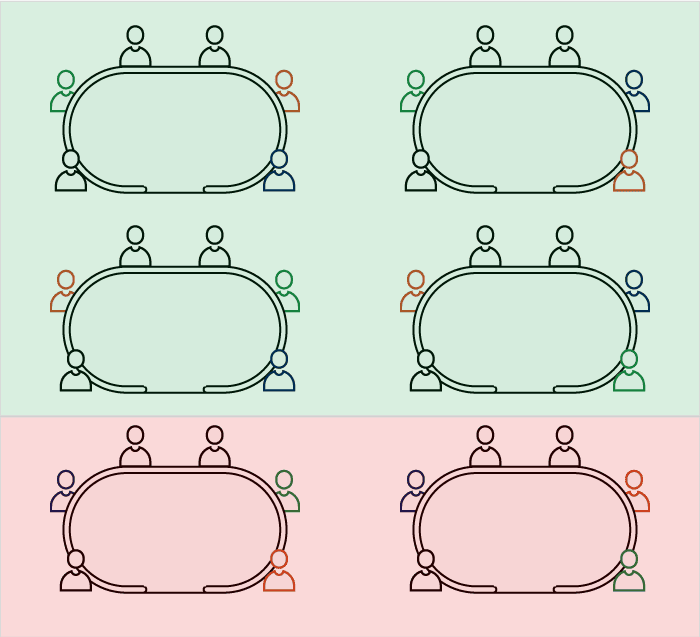
Ici, on voit que l'union de ces deux événements correspond à l'ensemble des résultats possibles de cette expérience.
Les deux événements n'ont aucun élément en commun et tous les résultats possibles sont couverts, on peut parler de partition.
Voici 2 nouveaux événements :
- : "Davidi s'assoit sur un des deux sièges à Droite de la table"
- : "Hero s'assoit sur un des deux sièges à Droite de la table"
L'intersection de deux événements est noté :
- "Davidi s'assoit sur un des deux sièges à droite de la table" ET (en même temps) "Hero s'assoit sur un des deux sièges à droite de la table"
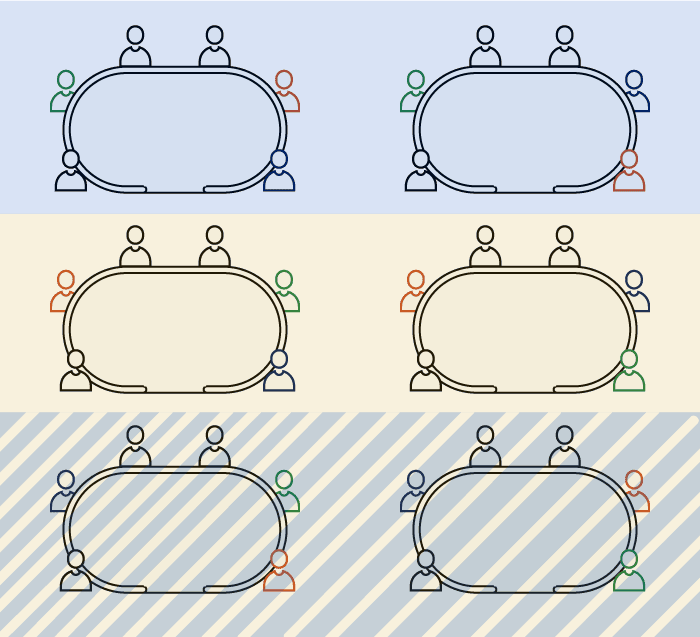
Ici encore, on voit que l'union de ces deux événements correspond à l'ensemble des résultats possibles de cette expérience.
Cependant les deux événements ont des éléments en commun, on parle de l'intersection de ces deux événements.
Il y a deux combinaisons où Hero et Davidi se situent à droite de la table.
La probabilité de
"Davidi s'assoit sur un des deux sièges à Droite de la table" estLa probabilité de "Hero s'assoit sur un des deux sièges à Droite de la table" est
La probabilité de l'intersection est
La probabilité de "s'asseoir à la table" est
Par définition, les éléments présents dans l'intersection (
) se situent dans l'événement et l'événement .et comprennent chacun la probabilité due aux éléments de l'intersection .
La somme de la probabilité de ces deux événements contient donc deux fois la probabilité due aux éléments de l'intersection.
On peut aussi remarquer que l'union des deux événements
et couvrent tout l'Univers ().On peut écrire :
Un événement ayant une probabilité de 1 est appelé un événement certain.
L'union d'un événement et de son événement contraire donne un événement certain.
Un événement et son événement contraire n'ont aucun élément en commun et donc une intersection vide, on dit qu'ils sont disjoints.
En général pour 3 événements A, B et C, si :
Alors :
Revenons à notre question de base : Quelle est la probabilité de ne pas s'asseoir à côté de Davidi ?
- avec D : "s'asseoir à côté de Davidi"
- avec ND : "Ne pas s'asseoir à côté de Davidi"
- avec A :"être Assis à la table"
Retrouver les mêmes résultats mathématiquement
Nos trois événements sont liés entre eux. On a :
Nous seront forcément assis à la table à l'issue de l'expérience aléatoire.
est un événement certain, donc
Déterminer le cardinal de l'Univers de notre expérience aléatoire
Le cardinal d'un ensemble est le nombre d'éléments contenus dans cet ensemble.
Si , alors
est composé des éléments , soit un total de 5 éléments.
Dans notre exemple, les éléments de notre Univers sont des triplets de la forme (Joueur sur le siège 1, sur le siège 2, sur le siège 3).
Par exemple : (Hero, Villain, Davidi) qui signifie :
- Hero sur le siège 1
- Villain sur le siège 2
- Davidi sur le siège 3
Nous devons déterminer le nombre total de combinaisons possibles lorsque l'on place 3 personnes sur 3 sièges.
La première étape consiste à placer un des trois joueurs sur un premier siège.
Chaque joueur correspond à une possibilité, ce qui nous fait 3 placements différents.
La seconde étape consiste à placer un des deux joueurs restant sur le deuxième siège.
Pour chacune des 3 possibilités, il y a deux nouvelles possibilités.
Ce qui nous fait un total de 3 x 2 placements différents à ce stade.
La dernière étape consiste à placer le joueur restant sur le dernier siège.
Il ne reste plus qu'une seule possibilité.
Ce qui fait un total de 3 x 2 x 1 = 6 placements différents.
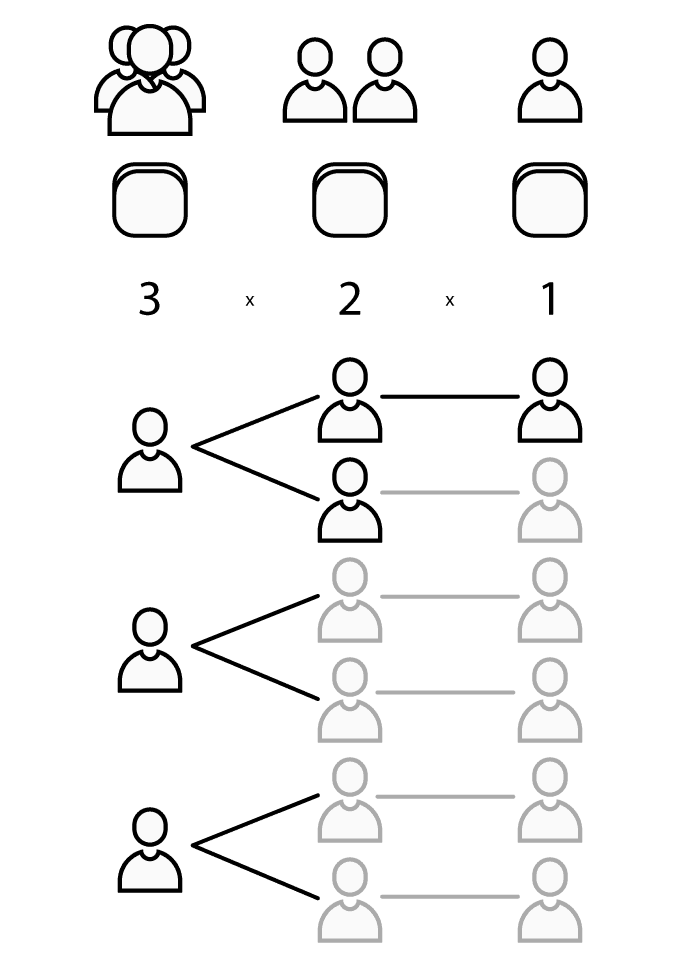
Nous avons donc 6 placements différents où 3 joueurs sont placés sur 3 sièges, ce qui équivaut à dire : le cardinal de l'Univers de notre expérience aléatoire est 6.
Déterminer le cardinal de D
Nous pouvons facilement déterminer les combinaisons où nous sommes assis à côté de Davidi sans énumérer tous les cas possibles.
À l'inverse, il est compliqué de calculer le nombre de combinaisons où nous ne sommes pas à côté de Davidi.
Pour cette raison, nous cherchons à calculer la probabilité d'être à côté de Davidi et il nous suffira de soustraire cette probabilité à 1 pour obtenir la probabilité de ne pas être à côté de Davidi.
La table de départ
On commence par séparer les 3 personnes à placer en deux groupe :
- Nous et Davidi
- L'autre Villain
Placer Villain
Nous pouvons placer Villain sur le siège de gauche. La personne sur ce siège se retrouvant forcément isolée des deux autres joueurs à placer. Nous ne pouvons donc ni y placer Davidi, ni nous-même.
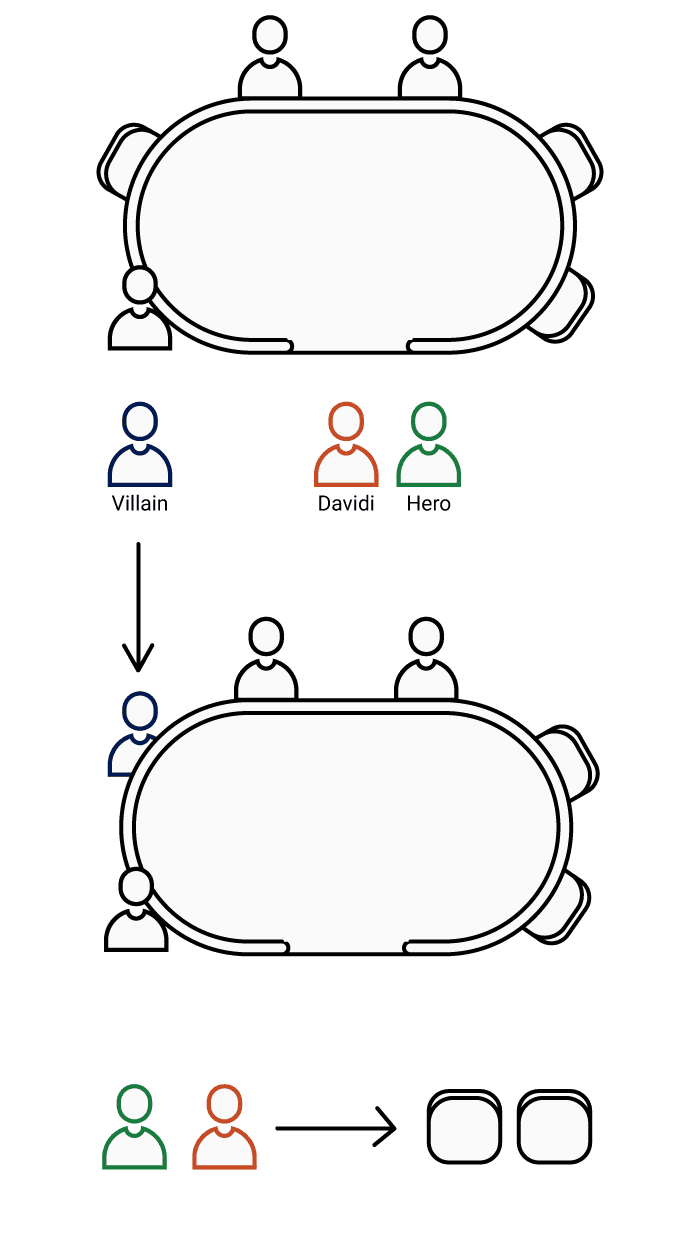
Calculer le nombre de placements restant
Une fois que Villain est placé, il ne reste plus que deux sièges côte à côte et Davidi et nous-même à placer. La notion d'ordre de placement étant présent, nous sommes dans le même cas que précédemment et trouvons : 2 x 1 = 2 placements possibles
L'événement D correspond à deux combinaisons, autrement dit
Déterminer la probabilité de D
L'événement D correspond à 2 combinaisons sur les 6 combinaisons qui composent l'Univers.
L'événement D va se produire 2 fois sur 6 ce qui correspond a une probabilité de
avec et
Déterminer la probabilité de ND
Maintenant que nous connaissons la probabilité de
, nous pouvons facilement trouver la probabilité de .Conclusion
La probabilité de l'événement
"Ne pas s'asseoir à côté de Davidi" est de 66,66%.2 fois sur 3, nous ne serons pas assis à côté de Davidi.
Résumé
- La notion de probabilité apparaît lors d'une expérience aléatoire.
- Un événement est un ensemble de résultats possibles.
- Le cardinal d'un événement est le nombre de résultats qui le compose.
Noté : - La probabilité d'un événement est la fréquence à laquelle l'événement va avoir lieu.
Noté : - Un événement est certain lorsque nous sommes certain qu'il se produira, c'est à dire qu'il a une probabilité de 1 (ou 100%).
- L'ensemble des résultats possibles d'une expérience aléatoire s'appelle l'Univers.
- L'union d'un événement et de son contraire ()est équivalent à l'Univers.
Je voudrais une paire de 10 ou mieux…
Nous allons essayer de déterminer la probabilité de se faire servir une paire de 10 ou plus lors d'unemain de poker en ligne qui est une bonne main de départ et qui peut permettre d'obtenir un brelan dès le flop comme combinaison.
Voici toutes les informations que nous avons :
- un paquet est composé de 52 cartes
- nous recevons 2 cartes du paquet
- les cartes sont distribuées aléatoirement
Un peu de formalisme :
- l'événement TT : se faire servir une paire de 10
- l'événement TT+ : se faire servir une paire de 10 ou plus (i.e. : paire de 10, de Valets, de Dames, de Rois ou d'As)
Première étape : tirer deux cartes parmi les 52 cartes du paquet
Pour commencer, nous devons calculer le nombre de combinaisons correspondant au tirage de 2 cartes parmi les 52 cartes du paquets.
Pour tirer deux cartes, il faut d'abord tirer une première carte puis une seconde.
Ça peut paraître évidement mais je préfère quand même le préciser.
Tirage d'une carte dans un paquet de 52 cartes
Un des tirages possibles serait de tirer l'As de coeur, un deuxième tirage serait de tirer le 2 de coeur... et ainsi de suite pour les 52 cartes du paquet.
On se rend bien compte qu'une carte correspond à un tirage possible. En ne tirant qu'une seule carte parmi les 52 cartes, le nombre de tirages possibles est de 52.
Tirage d'une carte dans un paquet de 51 cartes
Lorsque l'on tire la première carte, on ne la remet pas dans le paquet.
Lors du tirage de la seconde carte, il ne reste alors que 51 cartes dans le paquet. On a donc 51 tirages possibles.
Tirage de deux cartes dans un paquet de 52 cartes
Nous avons 52 tirages correspondant à tirer une première carte, puis pour chacun de ces tirages, nous avons 51 autres tirages possibles.
Cela revient à dire qu'il y a 52 fois 51 tirages possibles de deux cartes dans un paquet de 52. Soit
Arrangements et combinaisons
Lors de nos différentes étapes, une notion d'ordre est présente.
Tirer un As de coeur puis un Roi de coeur est différent de tirer un Roi de coeur puis un As de coeur or il s'agit de la même main.
La notion d'arrangements
Lorsque l'on choisit k éléments parmi n et que la notion d'ordre à de l'importance, on obtient un k-uplet (une liste ordonnée de k éléments). Ce k-uplet est un k-arrangement.
(lire «A» «n» «k») : le nombre de k-arrangements parmi n.
On note
Avec notre As de coeur et Roi de coeur, nous avons 2 arrangements pour une même main.
La notion de combinaison
Lorsque l'on choisit k éléments parmi n et que la notion d'ordre n'a pas d'importance, on obtient un ensemble de k éléments. Cet ensemble de k éléments est une k-combinaison.
(lire «C» «n» «k») ou (lire «k» parmi «n») : le nombre de k-combinaisons parmi n.
On note
Une main comme As de coeur et Roi de coeur est une 2-combinaison.
Deuxième étape : les combinaisons de deux cartes parmi les 52
Le cas du No Limit Holdem
Nous avons
tirages possibles de 2 cartes parmi 52.En tirant une première carte, puis une seconde carte, on introduit une notion d'ordre.
En réalité, ce que nous appelons "les tirages possibles" sont des 2-arrangements. C'est à dire, des arrangements composés de deux éléments.
Nous avons 2652 2-arrangements de 2 cartes parmi 52 cartes.
Une 2-combinaison (la main As de coeur et Roi de coeur) correspond à deux 2-arrangements (As de coeur / Roi de coeur et Roi de coeur / As de coeur).
Pour obtenir le nombre de 2-combinaisons, il faut diviser le nombre de 2-arrangements par 2.
On obtient 1326 combinaisons de mains différentes au NLHE.
Le cas du Pot Limit Omaha
Dans le cas du PLO, nous ne recevons pas 2 mais 4 cartes parmi 52 cartes !
L'objectif est de déterminer le nombre de combinaisons de mains différentes en PLO.
Cela revient à poser la question : 4 cartes sont tirées d'un jeu de poker de 52 cartes, combien de combinaison existe-t-il ?
Première étape : Trouver le nombre d'arrangements
Il y a 6 497 000 arrangements possibles de 4 cartes parmi 52.
Deuxième étape : Gérer la notion d'ordre
Nous avons 24 façons différentes d'ordonner 4 éléments. Une combinaison correspond à 24 arrangements.
Troisième étape : Trouver le nombre de combinaisons
On obtient 49 700 combinaisons de mains différentes en PLO.
Un peu de mathématiques
Le notion de factorielle
En mathématiques, la factorielle d'un entier naturel k est le produit des nombres entiers strictement positifs inférieurs ou égaux à k. (wikipedia.org)
(lire «k» factorielle)
Elle est notée :
Attention :
Essayons d'écrire nos arrangements grâce aux factorielles :
On a
Essayons d'écrire nos combinaisons grâce aux factorielles :
On a
Grâce aux formules, si on cherche à retrouver le nombre de combinaisons de mains au NLHE, il nous suffit de calculer
.On retrouve le même résultat qu'auparavant en seulement quelques calculs.
Ouf, on retombe sur nos pieds !
Peux-tu m'expliquer l'intérêt de tout ça ?...
Troisième étape : se faire servir une paire de 10
On veut connaitre la probabilité de se faire servir une paire de 10.
On cherche donc
L'Univers correspond à toutes les mains possibles du NLHE, soit 1326 mains différentes. Le cardinal de notre Univers est donc 1326.
On a
avecPour obtenir
, il faut trouver le nombre de combinaisons possibles pour former une paire de 10.Dans un paquet, il y a quatre 10. Une paire de 10 revient à avoir 2 cartes parmi ces 4, soit le nombre de combinaisons de 2 cartes parmi 4.
Il y a donc 6 mains pouvant former une paire de 10.
Nous avons donc
La probabilité d'obtenir une paire de 10 est de 0,45%.
Quatrième étape : se faire servir une paire de 10 ou mieux
Se faire servir une paire de 10 ou mieux revient à toucher une de ces cinq paires :
- TT
- JJ
- KK
- AA
On a vu que la paire de 10 correspond à 6 mains car il y a 4 cartes 10 dans le paquet. Toutes les paires étant composées de la même manière (2 cartes parmi 4), chacune des paires correspond à 6 mains.
Dans notre cas, on a :
Toucher paire de 10 ou plus correspond à 30 mains.
30 combos, tu sais, ça me parle pas beaucoup...
Pas de problème, on va transformer ça en pourcentage !
La probabilité d'obtenir une paire de 10 ou mieux est de 2,26%.
Et voilà, en deux ou trois mouvements, on vient de répondre à la question de départ !
Résumé
- Lorsque l'on veut tirer k élément parmi n élément avec une notion d'ordre au tirage, on obtient un k-arrangement qui est une liste ordonnée de k éléments par les n.
- On note , le nombre de k-arrangements de k éléments parmi n.
- Lorsque l'on veut tirer k élément parmi n élément sans une notion d'ordre au tirage, on obtient une k-combinaison qui est une liste non-ordonnée de k éléments par les n.
- On note , le nombre de k-combinaisons de k éléments parmi n.